I made a mistake. And I would like to apologize to everyone who was at the Institute faculty meeting of February 21, 2024. During that meeting I forgot to call for “no” votes on a motion to move to an executive session.
I know there are many people who (justifiably!) felt confused during the meeting and disenfranchised afterwards. I would have felt the same.
Following the rules of order is essential for the smooth functioning of a faculty meeting and I am mortified that I threw a spanner in the works. I sincerely apologize to my colleagues who were deprived of their right to vote; this is unacceptable, and I am deeply sorry that I was the cause of that injustice.
While I can’t change what happened at the meeting, I can try to ensure that this doesn’t happen again. For starters, I will work with the Chair of the Faculty to propose a set of guidelines to safeguard our parliamentary procedures (e.g., having a parliamentarian at the meeting could enable us to correct procedural errors in real-time). In addition, I have learned that it was difficult for the people on Zoom to understand what was happening in 10-250, which in turn made it difficult for them to participate in the discussion. Given these and other challenges we have faced with the hybrid meeting format, I hope that we as a faculty will have a serious discussion about whether the current format of the faculty meeting is best serving our needs.
Regardless of whether these steps turn out to be helpful, I deeply regret my mistake and I apologize to everyone who was in attendance at the meeting.
Second, I would like to send a special message to the students who were there. Your actions will be judged differently by different members of our community, but from my point of view at the podium, you showed respect for our rules of order. You observed the speaking privilege rules of the meeting; you followed the rules of the executive session; and you carried yourselves with dignity and decorum when you left the room. I saw and appreciated the care with which you treated our protocols and, by following the rules to a T, you evoked the sympathy of many people.
The rest of this letter is less important than the apology; however, for those of you who are willing to indulge me a bit longer, there are two questions that continue to haunt me: The first is about freedom of expression and the second is a math question. As many of you know, I am co-chairing the ad hoc Committee on Academic Freedom and Free Expression (CAFCE). The primary reason I agreed to do this, is that I am concerned by surveys that suggest people do not feel comfortable speaking up on the MIT campus. My concern has now grown into alarm. How can it be – given the egregious nature of my mistake at the faculty meeting – that not a single faculty member made a Point of Order to correct my error on the spot? There are many plausible explanations for why this might happen, but I worry that, for many years at MIT, we have allowed a climate to persist where people do not want to speak up in public. There is an enormous amount of wisdom in our faculty and a climate of silence makes that wisdom hard to access. I don’t know how to fix this, but let me start by saying that, as a Faculty Officer, I welcome your dissent. I am genuinely interested in your opinion. (And anyone who saves me from making another boneheaded blunder like the one I made on February 21 will have my eternal gratitude!)
Finally, I’d like to end on a question which has been the subject of much speculation: Would the outcome have been different if I had remembered to call for the no votes? To be clear, the answer to this question in no way mitigates my error. Voting is a form of expression regardless of the outcome, and all faculty have the right to express themselves through their vote at the faculty meeting. Nonetheless, given the interest around this question, and as one more form of atonement, let me share all the data I have managed to collect and offer a brief analysis. In the following I will provide an excess of data in case someone would like to perform their own analysis with different assumptions.
When we called for a quorum at the beginning of the meeting, there were 23 faculty in 10-250 and 24 faculty on Zoom who raised their hands. At the time of the vote, the number of faculty on Zoom was 46. These numbers are not speculative or approximate. They have been taken directly from the Zoom meeting log.[1] The number of yes votes in 10-250 was 22 and the number of yes votes on Zoom was 20 for a total of 42 yes votes. In addition, we know that throughout the meeting, 66 unique faculty were on Zoom at some point, albeit not all at the same time.
The next set of numbers can be estimated from historical data. In recent history, the number of faculty who attend each meeting lies roughly between 95 and 105. Both the Faculty Governance Administrator and I independently estimated the number of faculty in 10-250 to be approximately 40 ± 10. This estimate is also consistent with the historical data: 66 (faculty on Zoom) + 40 (faculty in 10-250) = 106 which is in-line with historical attendance numbers.
The final set of data I received from the Faculty Governance Administrator is the total number of people who voted in each of the last 10 votes at the faculty meeting: 63, 64, 64, 57, 61, 65, 69, 86, 83, 83. This yields a mean number of people voting of 69.5 and a standard deviation of 10.54.
Given that the total number of faculty at the meeting of February 21 was consistent with the number of faculty at recent meetings, one plausible way to estimate what the total number of votes would have been had the no vote been called, is to use the mean number of people voting in recent meetings. In that case, the expected number of no votes would be:
# no votes = mean(# total votes) – # yes votes = 69.5 – 42 = 27.5
which would not have been sufficient to overturn the yes vote.
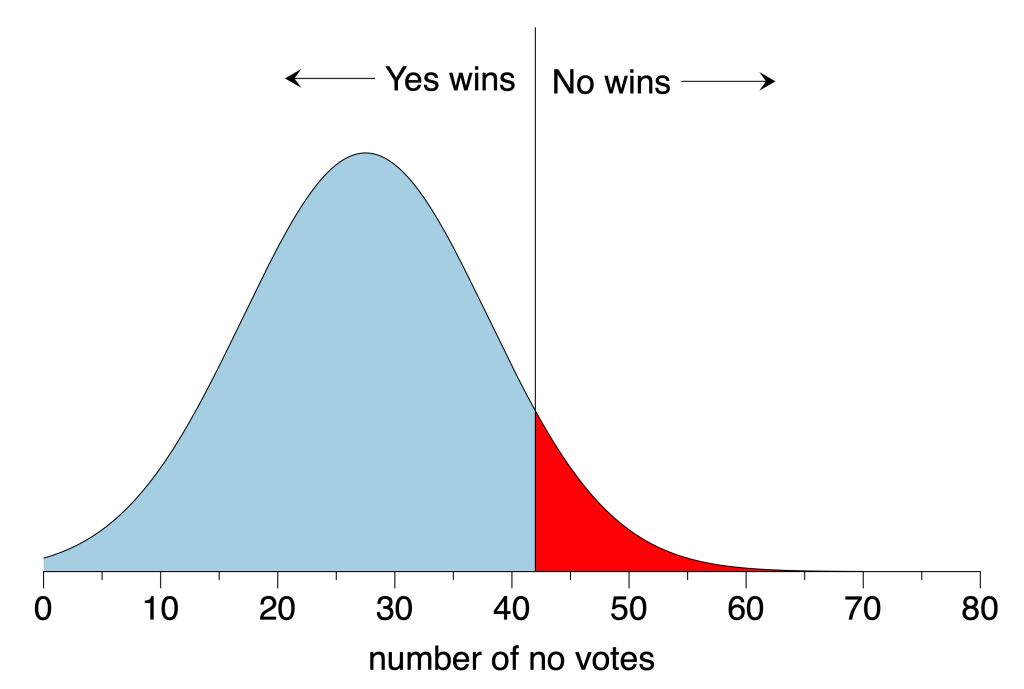
However, I would argue that this is not quite the right question to ask. A better question is what is the probability that the no votes would prevail? Suppose we model the total number of votes as a normally distributed random variable with the same mean and standard deviation as the measured data; then the distribution of no votes is the same but shifted to the left by 42 (i.e., we remove the known number of yes votes from the total). That distribution is shown in the figure. The area under the curve above 42 no votes (shown in red) represents the fraction of the time the no votes win if we replayed this scenario many times. The area under the curve below 42 no votes (shown in blue) similarly represents the fraction of the time the yeses would prevail. Integrating both areas and taking the ratio of the blue area to the total area, we find that there is a 92% chance that the yes votes would have won had we executed the vote properly.
So although it is not probable that the outcome would have changed had I remembered to call for the no vote, it is certainly possible. Which is of course why it is essential to count the votes. And why my mistake was so egregious.
Mea Culpa.
[1] There has been some speculation that there were 95 faculty on Zoom at the time of the vote. This is incorrect. There may have been 95 people on Zoom but only 46 were faculty with voting privileges.


